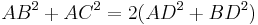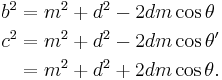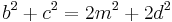Apollonius' theorem

In geometry, Apollonius' theorem is a theorem relating the length of a median of a triangle to the lengths of its side. Specifically, in any triangle ABC, if AD is a median, then

AB^2 %2B AC^2 = 2(AD^2%2BBD^2)\,

It is a special case of Stewart's theorem. For an isosceles triangle the theorem reduces to the Pythagorean theorem. From the fact that diagonals of a parallelogram bisect each other, the theorem is equivalent to the parallelogram law.

The theorem is named for Apollonius of Perga.

Proof

The theorem can be proved as a special case of Stewart's theorem, or can be proved using vectors (see parallelogram law). The following is an independent proof using the law of cosines.[1]

Let the triangle have sides a, b, c with a median d drawn to side a. Let m be the length of the segments of a formed by the median, so m is half of a. Let the angles formed between a and d be θ and θ′ where θ includes b and θ′ includes c. Then θ′ is the supplement of θ and cos θ′ = −cos θ. The law of cosines for θ and θ′ states

\begin{align} b^2 &= m^2 %2B d^2 - 2dm\cos\theta \\ c^2 &= m^2 %2B d^2 - 2dm\cos\theta' \\ &= m^2 %2B d^2 %2B 2dm\cos\theta.\, \end{align}

Add these equations to obtain

b^2 %2B c^2 = 2m^2 %2B 2d^2\,

as required.

See also

References

  1. ^ Following Godfrey & Siddons